ゼオライトの粒子分布の擂潰時間依存性

• 石川式擂潰機：D18S
• ふるい振とう機：FRITSCH製　analysette 3
• ステンレスふるい：サンポー製　目の大きさ：355μm、250μm、180μm、100μm、74μm、44μm、25μｍ
• デジタルはかり：A&D製　SH-1000
• 送風低温乾燥炉：東京理化製　WFO-420

（1）ゼオライトを乾燥炉で15分乾燥させる

（2）D18Sで15分撹拌擂潰する（30rpm)

（3）ふるいごとに被擂潰物（ゼオライト）を乾燥炉で15分乾燥させる

（4）ふるいごとに被擂潰物（ゼオライト）をデジタルはかりでふるいごと測定する

※事前にふるいの重量は測定しておく

（5）重量測定後に被擂潰物をまとめて、D18Sでさらに15分撹拌擂潰する（30rpm）

（6）（3）、（4）を繰り返す

（7）重量測定後に被擂潰物をまとめて、D18Sでさらに30分撹拌擂潰する（30rpm）

（8）（6）を再度行う

（9）重量測定後に被擂潰物をまとめて、D18Sでさらに60分撹拌擂潰する（30rpm）

（10）（8）を再度行う

目の大きさ250μmに入っている粒子は、355μm以下、250μmより大きい粒子となる。

そのため、階級値を302.5((355＋250)/2)と定義する。他の目の大きさも同様とする。

目の大きさ355μmの粒子については、355μm以上なので、階級値が算出できないため、データとして使用しない。

この階級値を粒子サイズとして、図にプロットする。

測定結果は以下の表1.となる

これを比率に換算して、プロットし、多項式で近似曲線を引いたのが図1.となる

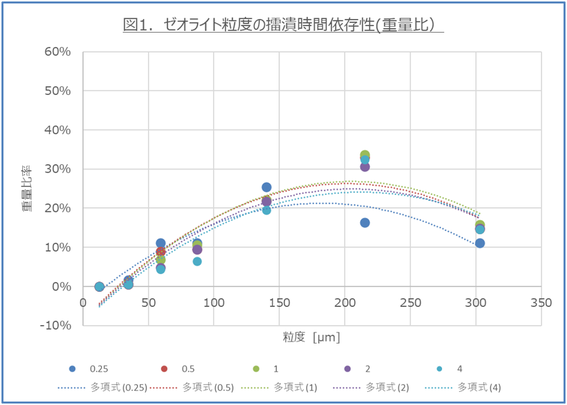
どの時間の近似曲線のピークは150μm程度にあり、かつ擂潰時間がながいほど、ピーク値が高いように見える

しかしながら、これは重量で粒子数の分布を正確に反映しているものではない。

そこで、重量分布を粒子数分布への変換を行う必要がある。

重量分布を粒子分布へ変換するには、単位粒子の重量で除する必要がある

そこで、密度はどの粒子でも一定と仮定して、各粒度の重量を体積で除したものの粒子数の比率が表2．となる

※粒度の1/2を半径として、3/4π（半径）^3 で重量を除したもの

それをプロットしたのもが図2．となる

図2のプロット図に対して、ガウス分布近似曲線を描画して、そのピーク値、ピーク幅から擂潰粒度とばらつきを推定する。その際に、ピーク値が粒子数分布が最も多いことになるので、ピーク値を擂潰粒子サイズとする。

また、ピーク幅が粒子サイズのばらつきを表わしているので、ピーク幅が小さいものほど、ばらつきが少なく、おおきいものほど、ばらつきが多いとする。

図3、図4はピーク値が同じため、擂潰粒子サイズは同じだが、ピーク幅が異なるために、擂潰粒子サイズのばらつきは図4の方が大きい。

図5に図2の0.25h（擂潰時間15分）のみをプロットする。このプロットを見ると、単純なガウス分布での近似曲線を引くことはできないので、複数のガウス曲線の和を用いて、近似曲線を描画することとする。

左側の山の近似曲線（近似曲線1）を赤色、右側の山の近似曲線（近似曲線2）を紫色で表示する。

プロット図に対して、ガウス分布近似曲線を描画して、そのピーク値、ピーク幅から擂潰粒子サイズとばらつきを推定する。

“近似曲線1”＋“近似曲線2”がガウス曲線での近似曲線となる。

近似曲線1のピーク値、ピーク幅を擂潰粒子サイズ、粒子サイズのばらつきと定義した。

分布がふた山になるのは、擂潰中の粒子の再凝集によるものと考えている。

左側の山が再凝集の山と推察している。

擂潰中には杵で擂潰物に圧力がかかるため、ふるい振とう機の振動では、放散しきれないものが再凝集としてカウントされると推察している。

近似曲線1より、各擂潰時間の擂潰粒子サイズ（μ）、及び粒子サイズのばらつき（σ）を算出した。

その結果を表3、図6、図7に示す。

粒子サイズも粒子サイズのばらつきも1時間程度の擂潰で数値が飽和する。

よって、D18Sでの擂潰においては、1時間程度の擂潰時間で十分であると推測できる。

その際の粒子サイズは、約45～50μm ばらつきは約11μm程度である。